Research

I aim to understand, diagnose and control nonlinear dynamical systems by blending operators theory with data-driven learning and control theory. The research problems are guided by applications in multi-agent robotic systems, network power systems, and transportation networks water.

Data-Driven Stochastic Optimal Control

The proposed framework relies on the linear operator theory involving linear Perron-Frobenius (P-F) and Koopman operators. The P-F operator provide a convex formulation to the optimal control problem in the dual space of densities. This convex formulation of the stochastic optimal control problem leads to an infinite-dimensional convex program. The finite-dimensional approximation of the convex program is obtained using a data-driven approximation of the P-F operator. On the other hand, we provide an iterative procedure along the lines of a popular policy iteration algorithm based on the data-driven approximation of the Koopman operator for solving the HJB equation. The two formulations, namely the convex formulation involving P-F operator and Koopman based formulation using HJB equation, can be viewed as dual to each other where the duality follows due to the dual nature of P-F and Koopman operators.

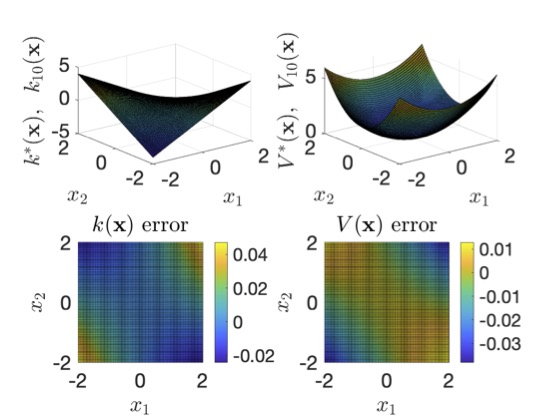Reachability Analysis

We demonstrate the application of spectral analysis of the Koopman operator involving eigenfunctions and eigenvalues in the approximate computation of forward and backward reachable sets for an autonomous dynamical system. The formal guarantees for the approximate reachable sets are provided using the Hausdorff distance between sets that measure how far the approximate reachable set is from the true reachable set. A computational framework based on convex optimization is provided to compute the Koopman spectrum and the approximate reachable set.
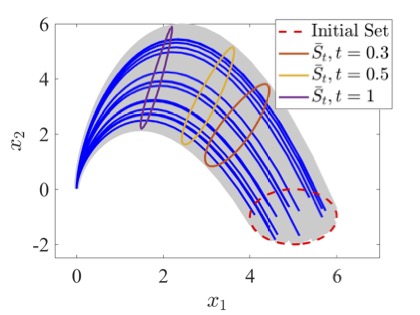